Week 3: Control Flow and Functions

Introduction to Computer Programming for Data Analysis I

Tom Paskhalis

11 May 2022

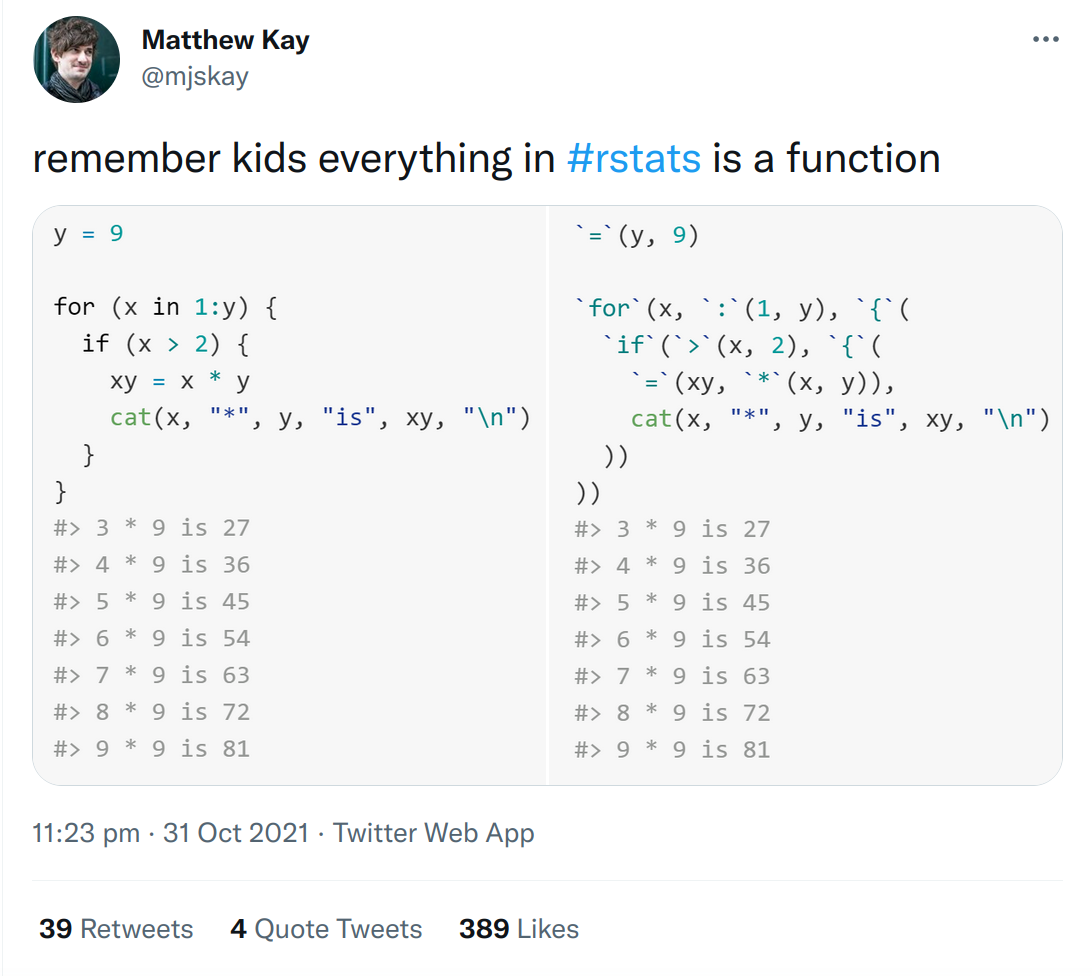
Overview

• Conditional statements
• Loops and Iteration
• Function definition and function call
• Functionals
• Scoping in R

Algorithm flowchart

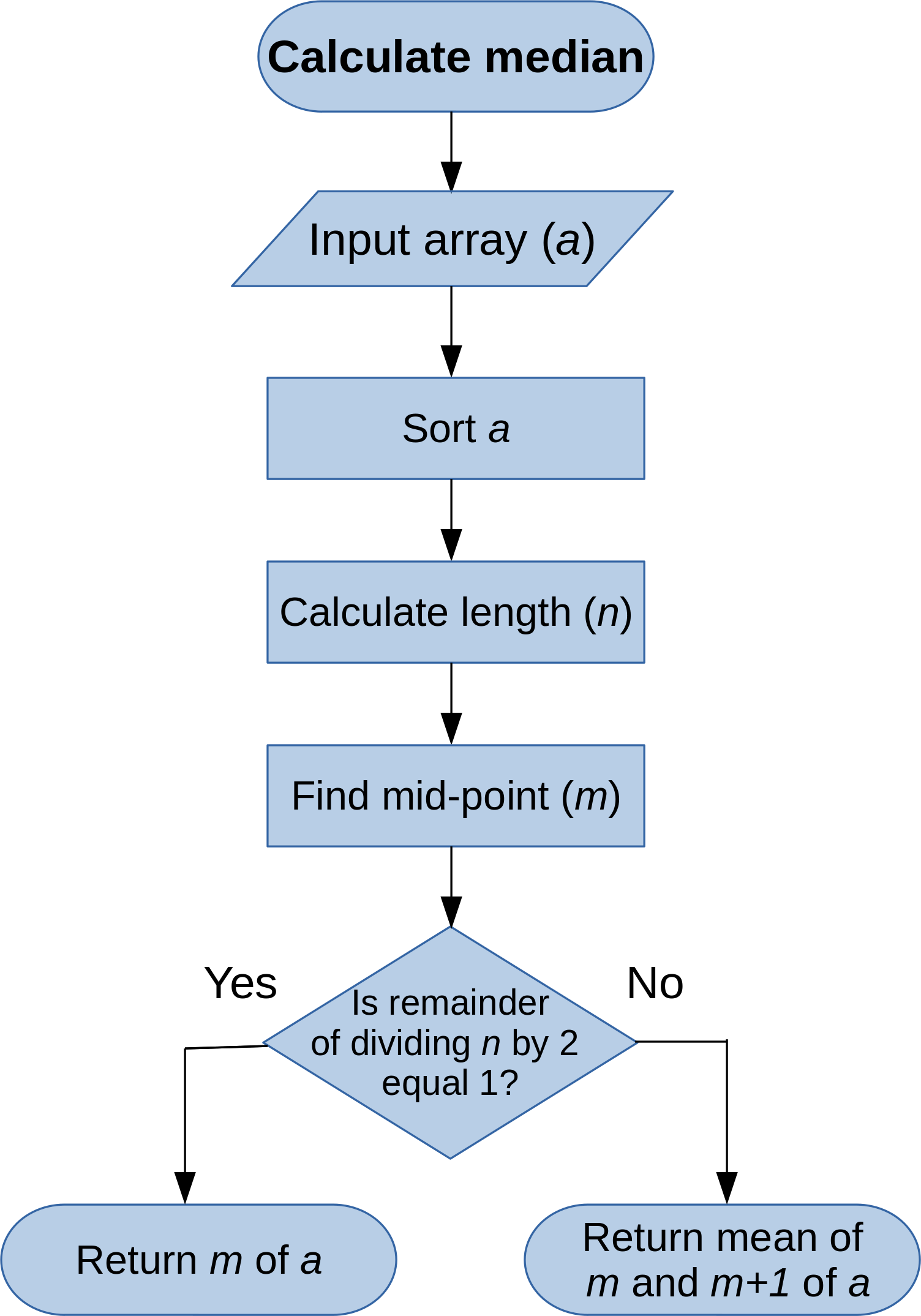
Algorithm flowchart (R)

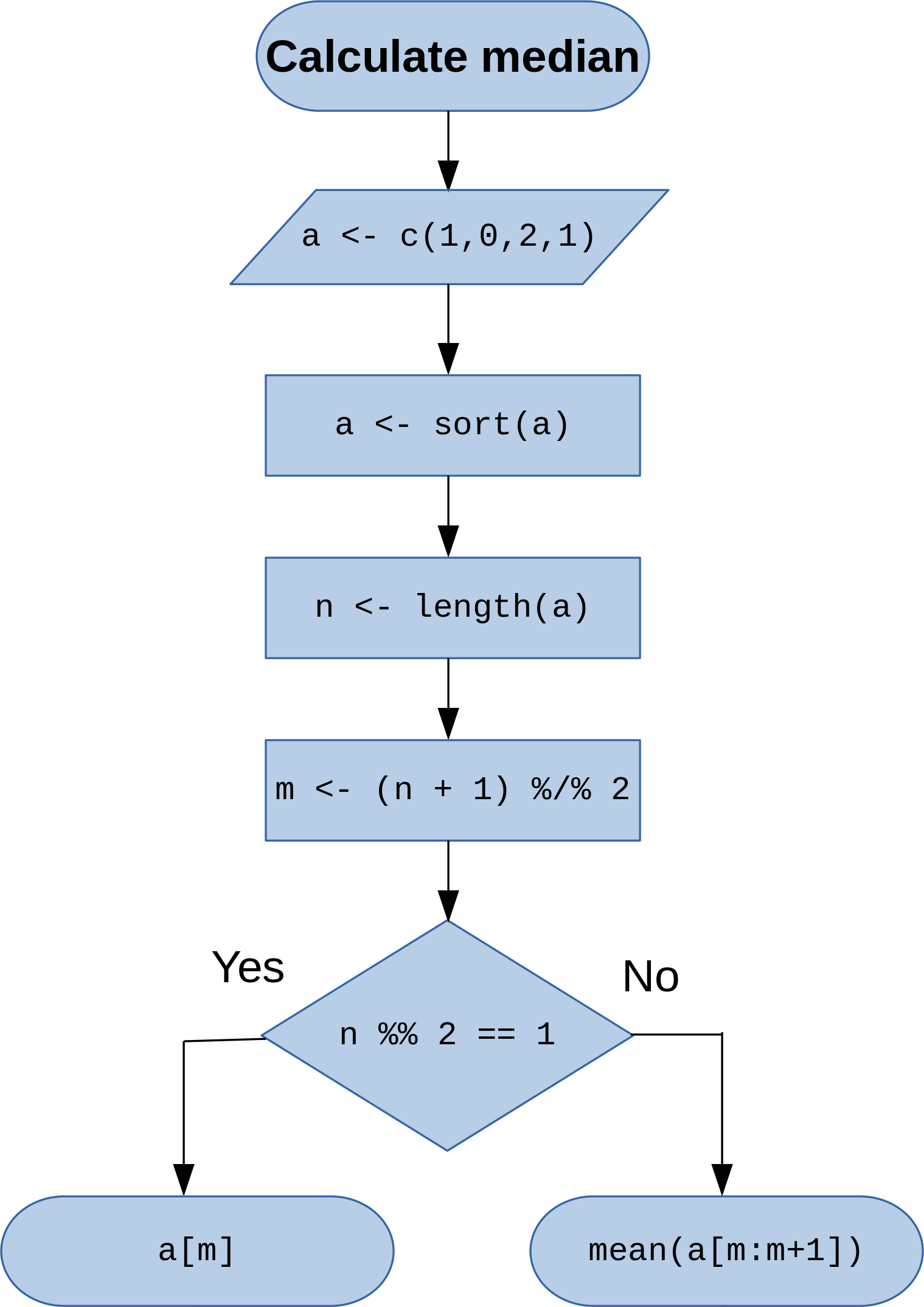
Calculate median

a <- c(1,0,2,1) # Input vector (1-dimensional array)
a <- sort(a) # Sort vector
a

[1] 0 1 1 2

n <- length(a) # Calculate length of vector 'a'
n

[1] 4

m <- (n + 1) %/% 2 # Calculate mid-point, %/% is operator for integer division 
m

[1] 2

n %% 2 == 1 # Check whether the number of elements is odd, %% (modulo) gives remainder of division

[1] FALSE

mean(a[m:m+1])

[1] 1

Control flow in R

• Control flow is the order in which statements are executed or evaluated
• Main ways of control flow in R:
  • Branching (conditional) statements (e.g. if)
  • Iteration (loops) (e.g. for)
  • Function calls (e.g. length())

Extra: R documentation on control flow

Branching programs

Conditional statements

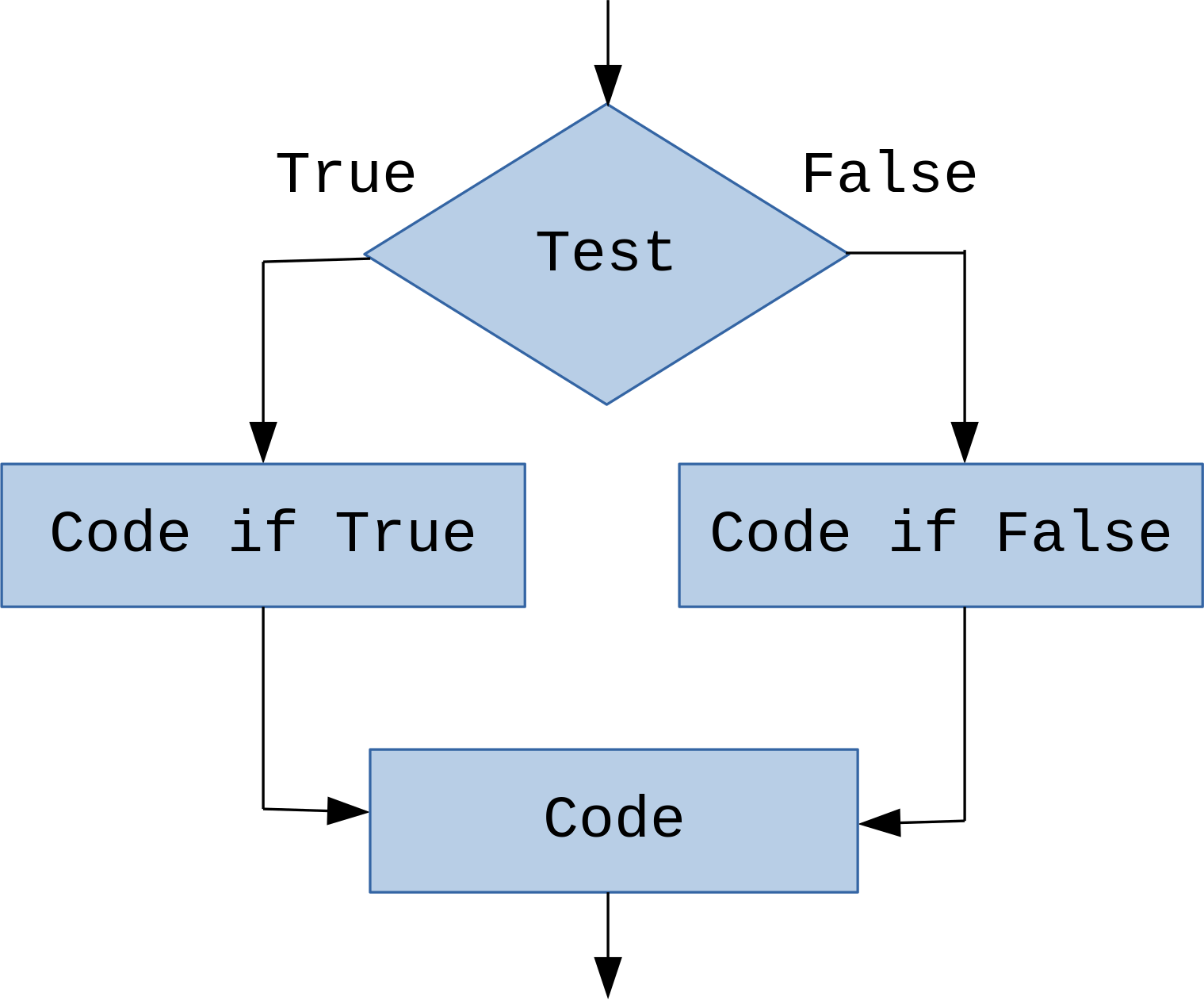
Conditional statements: if

• if - defines condition under which some code is executed

if (<boolean_expression>) {
  <some_code>
}

a <- c(1, 0, 2, 1, 100)
a <- sort(a)
n <- length(a)
m <- (n + 1) %/% 2
if (n %% 2 == 1) {
  a[m]
}

[1] 1

Conditional statements: if - else

• if - else - defines both condition under which some code is executed and alternative code to execute

if (<boolean_expression>) {
  <some_code>
} else {
  <some_other_code>
}

a <- c(1, 0, 2, 1)
a <- sort(a)
n <- length(a)
m <- (n + 1) %/% 2
if (n %% 2 == 1) {
  a[m]
} else {
  mean(a[m:m+1])
}

[1] 1

Conditional statements: if - else if - else

• if - else if - ... - else - defines both condition under which some code is executed and several alternatives

if (<boolean_expression>) {
  <some_code>
} else if (<boolean_expression>) {
  <some_other_code>
} else if (<boolean_expression>) {
...
...
} else {
  <some_more_code>
}

Example of longer conditional statement

x <- 42
if (x > 0) {
  print("Positive")
} else if (x < 0) {
  print("Negative")
} else {
  print("Zero")
}

[1] "Positive"

Optimising conditional statements

• Parts of conditional statement are evaluated sequentially, so it makes sense to put the most likely condition as the first one

# Ask for user input and cast as double
num <- as.double(readline("Please, enter a number:"))
if (num %% 2 == 0) {
  print("Even")
} else if (num %% 2 == 1) {
  print("Odd")
} else {
  print("This is a real number")
}

Please, enter a number:43
[1] "Odd"

Nesting conditional statements

• Conditional statements can be nested within each other
• But consider code legibility 📜, modularity ⚙️ and speed 🏎️

num <- as.integer(readline("Please, enter a number:")) # Ask for user input and cast as integer
if (num > 0) {
  if (num %% 2 == 0) {
    print("Positive even")
  } else {
    print("Positive odd")  
  }    
} else if (num < 0) {
  if (num %% 2 == 0) {
    print("Negative even") # Notice that odd/even check appears twice    
  } else {
    print("Negative odd") # Consider abstracting this as a function 
  }
} else {
  print("Zero")  
}

Please, enter a number:-43
[1] "Negative odd"

ifelse() function

• R also provides a vectorized version of if - else construct
• It takes a vector as an input and returns another vector as an output

ifelse(<boolean_expression>, <if_true>, <if_false>)

num <- 1:10
num

 [1]  1  2  3  4  5  6  7  8  9 10

ifelse(num %% 2 == 0, "even", "odd")

 [1] "odd"  "even" "odd"  "even" "odd"  "even" "odd"  "even" "odd"  "even"

Iteration (looping)

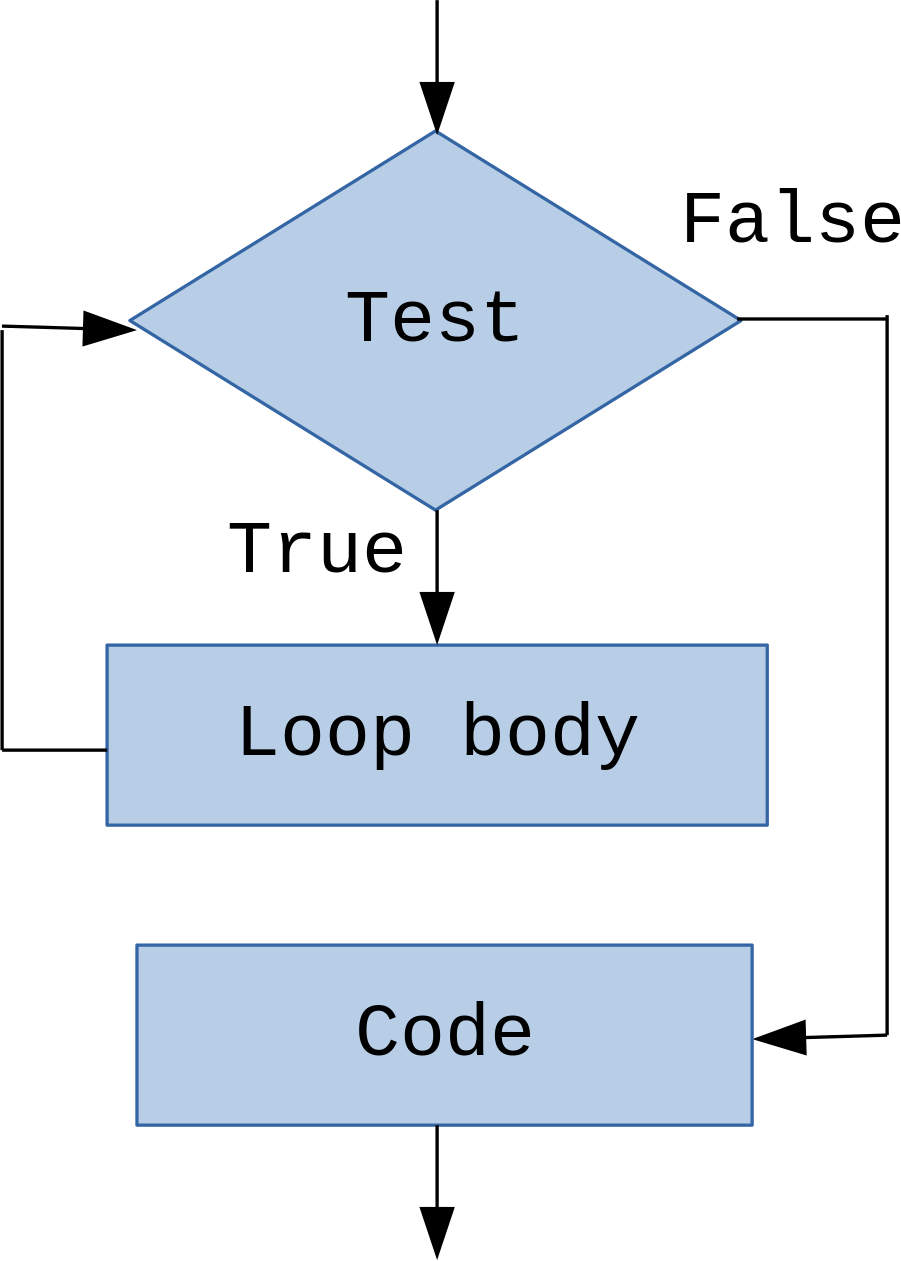
Iteration: while

• while - defines a condition under which some code (loop body) is executed repeatedly

while (<boolean_expression>) {
  <some_code>
}

# Calculate a factorial with decrementing function
# E.g. 5! = 1 * 2 * 3 * 4 * 5 = 120
x <- 5
factorial <- 1
while (x > 0) {
  factorial <- factorial * x
  x <- x - 1
}
factorial

[1] 120

Iteration: for

• for - defines elements and sequence over which some code is executed iteratively

for (<element> in <sequence>) {
  <some_code>
}

x <- seq(5)
factorial <- 1
for (i in x) {
  factorial <- factorial * i
}
factorial

[1] 120

Iteration with conditional statements

# Find maximum value in a vector with exhaustive enumeration
v <- c(3, 27, 9, 42, 10, 2, 5)
max_val <- v[1]
for (i in v) {
  if (i > max_val) {
    max_val <- i
  }
}
max_val

[1] 42

Generating sequences for iteration

• seq() function that we encountered in subsetting can be used in looping
• As well as its cousins: seq_len() and seq_along()

seq(<from>, <to>, <by>)
seq_len(<length>)
seq_along(<object>)

Generating sequences for iteration examples

# If by argument is omitted, it defaults to 1
s <- seq(25, 44)
s

 [1] 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44

# seq_len() is equivalent to seq(1, length(<object>))
seq_len(length(s))

 [1]  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20

seq_along(s)

 [1]  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20

# The sequence that you are supplying to seq_along() doesn't have to be numeric
seq_along(letters[1:20])

 [1]  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20

Generating sequences for iteration examples continued

# vector() function is useful for initiliazing empty vectors of known type and length
s2 <- vector(mode = "double", length = length(s))
for (i in seq_len(length(s))) {
    s2[i] <- s[i] * 2
}

s2

 [1] 50 52 54 56 58 60 62 64 66 68 70 72 74 76 78 80 82 84 86 88

s3 <- vector(mode = "double", length = length(s))
for (i in seq_along(s)) {
    s3[i] <- s[i] * 3
}

s3

 [1]  75  78  81  84  87  90  93  96  99 102 105 108 111 114 117 120 123 126 129
[20] 132

Iteration: break and next

• break - terminates the loop in which it is contained
• next - exits the iteration of a loop in which it is contained

for (i in seq(1,6)) {
  if (i %% 2 == 0) {
    break
  }
  print(i)
}

[1] 1

for (i in seq(1,6)) {
  if (i %% 2 == 0) {
    next
  }
  print(i)
}

[1] 1
[1] 3
[1] 5

Infinite loop

Infinite loops

• Loops that have no explicit limits for the number of iterations are called infinite
• They have to be terminated with a break statement (or Ctrl/Cmd-C in interactive session)
• Such loops can be unintentional (bug) or desired (e.g. waiting for user's input, some event)

i <- 1
while (TRUE) {
  i <- i + 1
  if (i > 10) {
    break
  }
}

i

[1] 11

Iteration: repeat

• repeat - defines code which is executed iteratively until the loop is explicitly terminated
• Is equivalent to while (TRUE)

repeat {
  <some_code>
}

i <- 1
repeat {
  i <- i + 1
  if (i > 10) {
    break
  }
}

i

[1] 11

Decomposition and abstraction

Source: IKEA

Decomposition and abstraction

• So far: built-in types, assignments, branching and looping constructs
• In principle, any problem can be solved just with those
• But a solution would be non-modual and hard-to-maintain
• Functions provide decomposition and abstraction

Functions

Source: xkcd

Functions in R

• Function call is the centerpiece of computation in R
• It involves function object and objects that are supplied as arguments
• Functions in R do not have side-effects (nonlocal modifications of input objects)
• In R we use function function() to create a function object
• Functions are also referred to as closures in some R documentation

<function_name> <- function(<arg_1>, <arg_2>, ..., <arg_n>) {
  <function_body>
}

foo <- function(arg) {
  # <function_body>
}

Function components

• Body (body()) - code inside the function
• List of arguments (formals()) - controls how function is called
• Environment/scope/namespace (environment()) - location of function's definition and variables

Function components example

is_positive <- function(num) {
  if (num > 0) {
    return(TRUE)
  } else {
    return(FALSE)
  }
}

body(is_positive)

{
    if (num > 0) {
        return(TRUE)
    }
    else {
        return(FALSE)
    }
}

formals(is_positive)

$num

environment(is_positive)

<environment: R_GlobalEnv>

Function call

• Function is executed until:
  • Either return() function is encountered
  • There are no more expressions to evaluate
• Function call always returns a value:
  • Argument of return() function call
  • Value of last expression if no return() (implicit return)
• Function can return only one object
  • But you can combine multiple R objects in a list

Function call example

is_positive <- function(num) {
  if (num > 0) {
    res <- TRUE
  } else {
    res <- FALSE
  }
  return(res)
}

res_1 <- is_positive(5)
res_2 <- is_positive(-7)

print(res_1)
print(res_2)

[1] TRUE
[1] FALSE

Implicit return example

is_positive <- function(num) {
  if (num > 0) {
    res <- TRUE
  } else {
    res <- FALSE
  }
  res
}

res_1 <- is_positive(5)
res_2 <- is_positive(-7)

print(res_1)
print(res_2)

[1] TRUE
[1] FALSE

Implicit return example continued

# While this function provides the same functionality as the two versions above
# This is an example of a bad programming style, return value is very unintuitive
is_positive <- function(num) {
  if (num > 0) {
    res <- TRUE
  } else {
    res <- FALSE
  }
}

res_1 <- is_positive(5)
res_2 <- is_positive(-7)

print(res_1)
print(res_2)

[1] TRUE
[1] FALSE

Function arguments

• Arguments provide a way of giving input to a function
• Arguments in function definition are formal arguments
• Arguments in function invocations are actual arguments
• When a function is invoked (called) arguments are matched and bound to local variable names
• R matches arguments in 3 ways:
  1. by exact name
  2. by partial name
  3. by position
• It is a good idea to only use unnamed (positional) for the main (first one or two) arguments

Function arguments example

format_date <- function(day, month, year, reverse = TRUE) {
  if (isTRUE(reverse)) {
    formatted <- paste(
      as.character(year), as.character(month), as.character(day), sep = "-"
    )
  } else {
    formatted <- paste(
      as.character(day), as.character(month), as.character(year), sep = "-"
    )
  }
  return(formatted)
}

format_date(4, 10, 2021)

[1] "2021-10-4"

format_date(y = 2021, m = 10, d = 4) # Technically correct, but rather unintuitive

[1] "2021-10-4"

format_date(y = 2021, m = 10, d = 4, FALSE) # Technically correct, but rather unintuitive

[1] "4-10-2021"

format_date(day = 4, month = 10, year = 2021, FALSE)

[1] "4-10-2021"

Nested functions

which_integer <- function(num) {
  even_or_odd <- function(num) {
    if (num %% 2 == 0) {
      return("even")
    } else {
      return("odd")
    }
  }
  eo <- even_or_odd(num)
  if (num > 0) {
    return(paste0("positive ", eo))
  } else if (num < 0) {
    return(paste0("negative ", eo))
  } else {
    return("zero")
  }
}

which_integer(-43)

[1] "negative odd"

even_or_odd(-43)

Error in even_or_odd(-43): could not find function "even_or_odd"
Traceback:

R environment basics

• Variables (aka names) exist in an environment (aka namespace/scope in Python)
• The same R object can have different names
• Binding of objects to names (assignment) happens within a specific environment
• Most environments get created by function calls
• Approximate hierarchy of environments:
  • Execution environment of a function
  • Global environment of a script
  • Package environment of any loaded packages
  • Base environment of base R objects

R environment example

x <- 42
# is equivalent to:
# Binding R object '42', double vector of length 1, to name 'x' in the global environment
assign("x", 42, envir = .GlobalEnv)
x

[1] 42

x <- 5
foo <- function() {
  x <- 12
  return(x)
}
y <- foo()
print(y)
print(x)

[1] 12
[1] 5

Every operation is a function call

Source: Twitter

Examples of operators as function calls

`+`(3, 2) # Equivalent to: 3 + 2

[1] 5

`<-`(x, c(10, 12, 14)) # x <- c(10, 12, 14)
x

[1] 10 12 14

`[`(x, 3) # x[3]

[1] 14

`>`(x, 10) # x > 10

[1] FALSE  TRUE  TRUE

Anonymous functions

• While R has no special syntax for creating anonymous (aka lambda in Python) function
• Note that the result of function() does not have to be assigned to a variable
• Thus function function() can be easily incorporate into other function calls

add_five <- function() {
  return(function(x) x + 5)
}
af <- add_five()

af # 'af' is just a function, which is yet to be invoked (called)

function(x) x + 5
<environment: 0x55baf8cccac0>

af(10) # Here we call a function and supply 10 as an argument

[1] 15

# Due to vectorized functions in R this example is an obvious overkill (seq(10) ^ 2 would do just fine)
# but it shows a general approach when we might need to apply a non-vectorized functions
sapply(seq(10), function(x) x ^ 2)

 [1]   1   4   9  16  25  36  49  64  81 100

Functionals

• Functionals are functions that take other functions as one of their inputs
• Due to R's functional nature, functionals are frequently used for many tasks
• apply() family of base R functionals is the most ubiquitous example
• Their most common use case is an alternative of for loops
• Loops in R have a reputation of being slow (not always warranted)
• Functionals also allow to keep code more concise

Functional example

# Applies a supplied function to a random draw
# from the normal distribution with mean 0 and sd 1
functional <- function(f) { f(rnorm(10)) }

functional(mean)

[1] 0.3186378

functional(median)

[1] -0.2481884

functional(sum)

[1] 1.492055

Summary of common apply() functions

Function	Description	Input Object	Output Object	Simplified
apply()	Apply a given function to margins (rows/columns) of input object	matrix/array/data.frame	vector/matrix/array/list	Yes
lapply()	Apply a given function to each element of input object	vector/list	list	No
sapply()	Same as lapply(), but output is simplified	vector/list	vector/matrix	Yes
vapply()	Same as sapply(), but data type of output is specified	vector/list	vector	No
mapply()	Multivariate version of sapply(), takes multiple objects as input	vectors/lists	vector/matrix	Yes

Extra: Using apply, sapply, lapply in R

lapply() function

• Takes a function and a vector or list as input
• Applies the input function to each element in the list
• Returns list as an onput

lapply(<input_object>, <function_name>, <arg_1>, ..., <arg_n>)

lapply() examples

l <- list(a = 1:2, b = 3:4, c = 5:6, d = 7:8, e = 9:10)

# Apply sum() to each element of list 'l'
lapply(l, sum)

$a
[1] 3

$b
[1] 7

$c
[1] 11

$d
[1] 15

$e
[1] 19

# We can exploit the fact that basic operators are function calls
# Here, each subsetting operator `[` with argument 2 is applied to each element
# Which gives us second element within each element of the list
lapply(l, `[`, 2)

$a
[1] 2

$b
[1] 4

$c
[1] 6

$d
[1] 8

$e
[1] 10

apply() function

• Works with higher-dimensional (> 1d) input objects (matrices, arrays, data frames)
• Is a common tool for calculating summaries of rows/columns
• <margin> argument indicates whether function is applied across rows (1) or columns (2)

apply(<input_object>, <margin>, <function_name>, <arg_1>, ..., <arg_n>)

apply() examples

m <- matrix(1:12, nrow = 3, ncol = 4)
m

     [,1] [,2] [,3] [,4]
[1,] 1    4    7    10  
[2,] 2    5    8    11  
[3,] 3    6    9    12  

# Sum up rows (can also be achieved with rowSums() function)
apply(m, 1, sum)

[1] 22 26 30

# Calculate averages across columns (also available in colMeans())
apply(m, 2, mean)

[1]  2  5  8 11

# Find maximum value in each column
apply(m, 2, max)

[1]  3  6  9 12

mapply() function

• Takes a function and multiple vectors or lists as input
• Applies the function to each corresponding element of input sequences
• Simplifies output into vector (if possible)

mapply(<function_name>, <input_object_1>, ..., <input_object_n>, <arg_1>, ..., <arg_n>)

mapply() examples

means <- -2:2
sds <- 1:5

# Generate one draw from a normal distribution where
# each mean is an element of vector 'means'
# and each standard deivation is an element of vector 'sds'
#
# rnorm(n, mean, sd) takes 3 arguments: n, mean, sd

mapply(rnorm, 1, means, sds)

[1] -0.7043966 -2.9181125  0.7705752  0.8115289  4.9755344

# While simplification of output
# (attempt to collapse it in fewer dimensions)
# makes hard to predict the object returned 
# by apply() functions that have simplified = TRUE by default

mapply(rnorm, 5, means, sds)

     [,1]      [,2]       [,3]        [,4]       [,5]      
[1,] -3.058834 -1.0853410 -0.08222913 -0.6397508  1.8098831
[2,] -2.759082 -3.6308276 -1.53727082  1.4870609 -0.4620664
[3,] -1.633935 -0.1775828 -3.99636499  2.7069711  4.1554896
[4,] -1.241012 -1.8139769 -0.35165313  5.2904383 11.1715264
[5,] -1.227846 -1.5496606  2.82421174  5.9838118  4.9411164

Packages

• Program can access functionality of a package using library() function
• Every package has its own namespace (which can accessed with ::)

library(<package_name>)
<package_name>::<object_name>

Package loading example

# Package 'Matrix' is part of the standard R library and doesn't have to be installed separately
library("Matrix")

# While it is possible to just use function sparseVector() after loading the library,
# it is good practice to state explicitly which package the object is coming from.
sv <- Matrix::sparseVector(x = c(1, 2, 3), i = c(3, 6, 9), length = 10)

sv

sparse vector (nnz/length = 3/10) of class "dsparseVector"
 [1] . . 1 . . 2 . . 3 .

Next

• Data wrangling