Week 3: Distributions & Sampling

POP88162 Introduction to Quantitative Research Methods

Working with Vectors

Let’s start by generating a random draw from a standard normal distribution

draws <- rnorm(100)

Check the top and bottom of this vector. Functions head() and tail() are applicable to different data structures in R. And printing out all 100 elements of this vector might be too verbose.

head(draws)

[1] -1.66002783  0.18846405  0.20485182  1.58559918  0.01295234  0.96525154

tail(draws)

[1]  0.43852609  1.09015686  1.20955951  0.09049652  1.09498017 -0.87159689

Let’s practice more vector subsetting. How many of the numbers in this random draw are larger than 1?

draws > 1

  [1] FALSE FALSE FALSE  TRUE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
 [13] FALSE  TRUE  TRUE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
 [25] FALSE FALSE FALSE FALSE FALSE  TRUE FALSE FALSE FALSE FALSE FALSE FALSE
 [37] FALSE FALSE FALSE  TRUE FALSE FALSE FALSE FALSE  TRUE FALSE FALSE FALSE
 [49] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE  TRUE  TRUE
 [61] FALSE FALSE FALSE  TRUE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
 [73] FALSE FALSE  TRUE FALSE  TRUE FALSE FALSE FALSE  TRUE FALSE FALSE FALSE
 [85] FALSE FALSE FALSE  TRUE FALSE FALSE FALSE FALSE FALSE FALSE FALSE  TRUE
 [97]  TRUE FALSE  TRUE FALSE

draws[draws > 1]

 [1] 1.585599 1.209981 1.211327 2.260458 2.053177 1.700086 1.558853 2.130747
 [9] 1.978007 1.325921 1.088110 1.341324 1.107506 1.090157 1.209560 1.094980

length(draws[draws > 1])

[1] 16

What proportion of random numbers is smaller than -3?

Working with Distributions

Let’s plot the density of a standard normal distribution. First, let’s, replicate the plot from the workshop by using dnorm() function.

x <- seq(-5, 5, 0.1)
plot(x, dnorm(x), type = "l")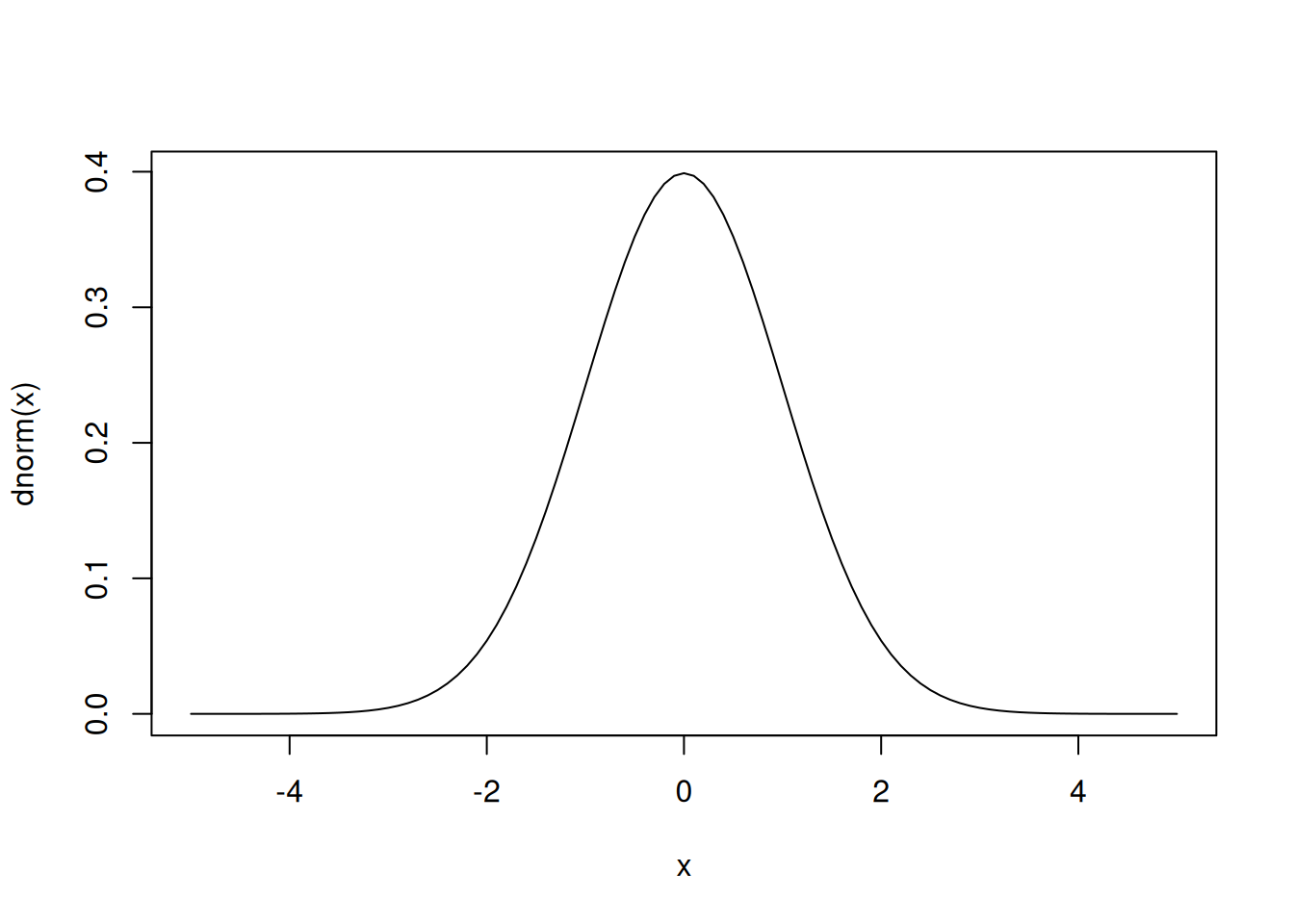

We can also get this plot by using random draws from above and built-in density() function in R. You can see that this plot is not nearly as pretty as the one above. This is due to a limited size of a random draw (only 100 observations). Try increasing the size of a random draw to check whether you can make this plot look closer to an ‘ideal’ normal distribution.

dens <- density(draws)
plot(dens)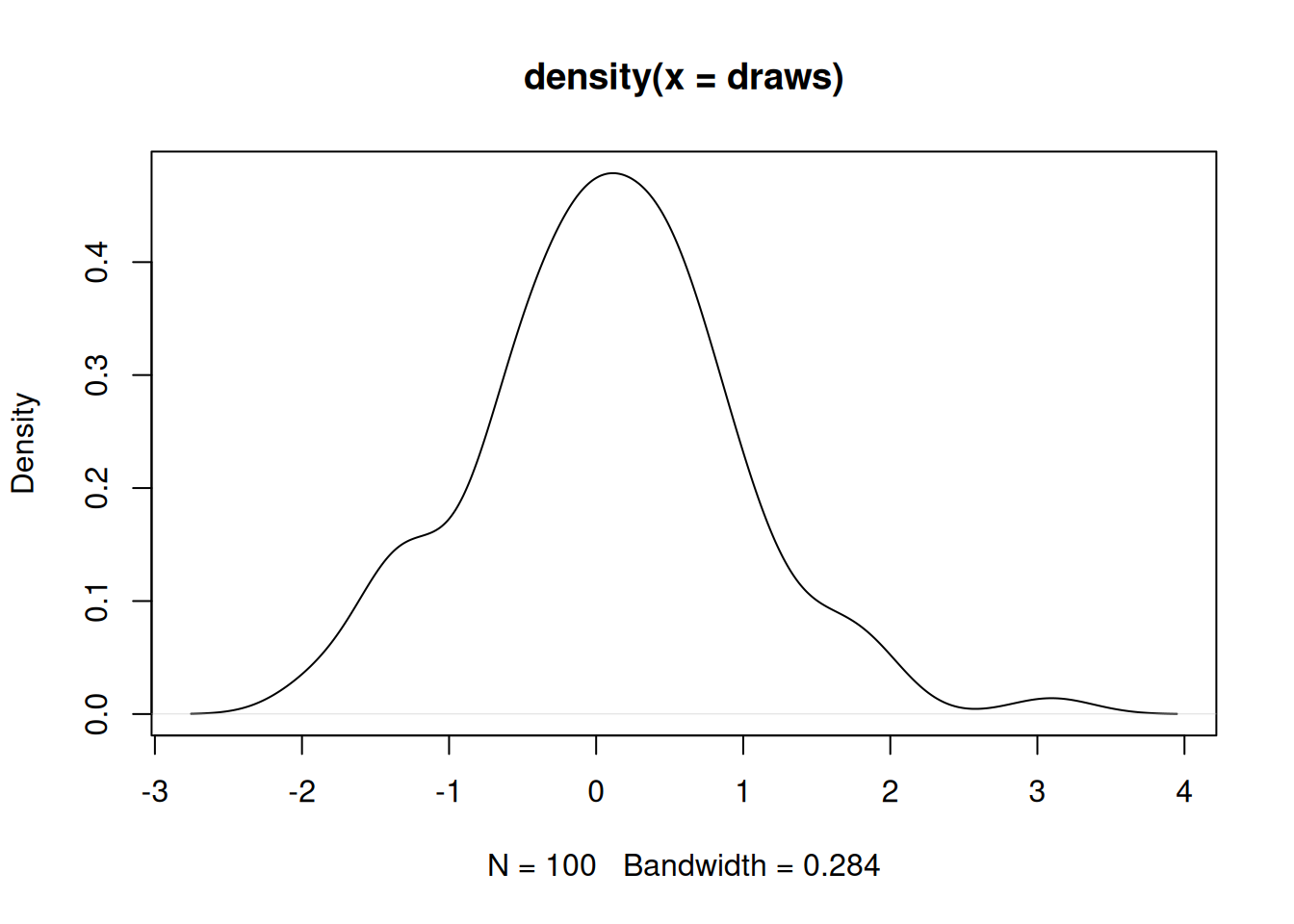

Plot a normal distribution with mean 10 and standard deviation 3.

Calculating probability

Following the example from the workshop, calculate the probability of observing a value larger than 2 for a variable that has a standard normal distribution.

Sampling

Function sample() often comes in handy when we need to draw a random sample from a dataset or an individual variable.

# Here, we are drawing a random sample of 5 from the vector `draws` created above
sample(draws, size = 5)

[1]  0.4198560  0.3019571  1.0949802 -1.6685290  1.5588534

Here is how we can draw a random sample from a data frame.

# Function with() tells R to obtain the variable names from `dens` object
# Otherwise, we would have needed to write its name twice and use $ subsetting
# as it is a list.
dd <- with(dens, data.frame(x, y))

# We are instructing R to draw a random sample of 10
# from the vector of row indices 1:nrow(dd)
dd[sample(1:nrow(dd), 10),]

              x            y
89  -1.72687504 0.0851513108
457  2.48974920 0.0241440415
121 -1.36021206 0.1690341520
26  -2.44874278 0.0027501719
219 -0.23730670 0.4143460547
38  -2.31124416 0.0073997443
322  0.94288976 0.2198762721
249  0.10643984 0.4373848323
247  0.08352341 0.4371785352
505  3.03974366 0.0004884356

Read in democracy_2020.csv dataset. Draw a random sample of 50 regimes.